martes, 3 de noviembre de 2015

Escalas termométricas

 ESCALAS TERMOMÉTRICAS

La temperatura es un concepto que involucra valores positivos y negativos, la asociamos al concepto "fiebre" cuando estamos enfermos, pero la verdad que mucho más amplio. Está presente en nuestra vida cotidiana y no nos damos cuenta. Usted puede enumerar, fácilmente tres situaciones donde se esté presente la temperatura.

Para medir la temperatura existe un instrumento llamado termómetro. Este instrumento está formado por un capilar muy fino en el interior de un tubo de vidrio, ambos extremos están cerrados y en uno de ellos se estrecha y el capilar tiene un bulbo con mercurio, el cual se dilata al más mínimo cambio de temperatura.

external image images?q=tbn:ANd9GcSyeECbqIItpJDR4HotjeuKBpyqbhcJjvefMnBWlIDA4kTRGr4&t=1&usg=__9TiiSzPX1UeFgCAz0OTBn1eAr5w=
Existen tres escalas termométricas conocidas y estas son:
  1. ESCALA CELSIUS O CENTÍGRADA: Es la más usada, toma como referencia el punto de fusión del agua para indicar la temperatura mínima, es decir 0 ºC, y considera el punto de ebullición del agua para indicar la temperatura más alta, o sea 100 ºC. Es una escala que considera valores negativos para la temperatura, siendo el valor más bajo de -273 ºC.
  2. ESCALA FAHRENHEIT O ANGLOSAJONA: Es una escala que tiene 180º de diferencia entre el valor mínima y el máximo del termómetro. También relaciona los puntos de fusión y ebullición del agua para indicar los valores de temperatura. El valor mínimo es a los 32 ºF y el máximo a los 212 ºF. Al igual que la escala Celsius, tiene valores negativos de temperatura.
  3. ESCALA KELVIN O ABSOLUTA: Es una escala que no tiene valores negativos. El punto de fusión del agua en esta escala es a los 273 ºK y el punto de ebullición es a los 373 ºK y la mínima temperatura es 0º K que para la escala Centígrada resulta ser a los -273 ºK.


ECUACIONES QUE RELACIONAN LAS DIFERENTES ESCALAS.

a) entre las escalas Celsius y Kelvin:

ºK = ºC + 273 ºC = ºK - 273

 b) entre las escalas Celsius y Fahrenheit:

ºC = 5

(ºF - 32) 9

 Lo particular de esta ecuación es que se puede transformar de Celsius a Fahrenheit y vis y versa.





TIPOS DE TERMÓMETROS.

Según el enlace hay una gran variedad de termómetros, muchos de los cuales aún no son conocidos por la gran mayoría de los estudiantes. ¿puede usted realizar algún tipo de clasificación?. Ésta podría ser por función, época de invención, por construcción, o usted puede encontrar otra forma de clasificación. INTÉNTELO!!

Publicado por en No hay comentarios:

TEOREMA DE TORRICELLI


Teorema de Torricelli

Evangelista Torricelli
Faenza, actual Italia, 1608-Florencia, 1647) Físico y matemático italiano. Se atribuye a Evangelista Torricelli la invención del barómetro. Asimismo, sus aportaciones a la geometría fueron determinantes en el desarrollo del cálculo integral.
Su tratado sobre mecánica De mutu (Acerca del movimiento), logró impresionar a Galileo, en quien el propio Torricelli se había inspirado a la hora de redactar la obra. En 1641 recibió una invitación para actuar como asistente de un ya anciano Galileo en Florencia, durante los que fueron los tres últimos meses de vida del célebre astrónomo de Pisa.
A la muerte de Galileo, Torricelli fue nombrado profesor de matemáticas de la Academia Florentina. Dos años más tarde, atendiendo una sugerencia formulada por Galileo, llenó con mercurio un tubo de vidrio de 1,2 m de longitud, y lo invirtió sobre un plato; comprobó entonces que el mercurio no se escapaba, y observó que en el espacio existente por encima del metal se creaba el vacío.
Tras muchas observaciones, concluyó que las variaciones en la altura de la columna de mercurio se deben a cambios en la presión atmosférica. Nunca llegó a publicar estas conclusiones, dado que se entregó de lleno al estudio de la matemática pura, incluyendo en su labor cálculos sobre la cicloide y otras figuras geométricas complejas.
En su título Opera geometrica, publicado en 1644, expuso también sus hallazgos sobre fenómenos de mecánica de fluidos y sobre el movimiento de proyectiles.
Teorema de Torricelli
La velocidad del chorro que sale por un único agujero en un recipiente es directamente proporcional a la raíz cuadrada de dos veces el valor de la aceleración de la gravedad multiplicada por la altura a la que se encuentra el nivel del fluido a partir del agujero.
Matemáticamente se tiene:
 
v = raíz cuadrada ((2 * g) * (h))
 
 
Ejemplo de aplicación del teorema de Torricelli (vaciado de un recipiente):
Un depósito cilíndrico, de sección S1 tiene un orificio muy pequeño en el fondo de sección S2 mucho más pequeña que S1 :
Aplicamos el teorema de Bernoulli suponiendo que lavelocidad del fluido en la sección mayor ,
 
 
 
 
Aplicamos el teorema de Bernoulli suponiendio que la velocidad del fluido en la sección s1 es despreciable, v1 es más o menos 0 comparada con la velocidad del fluido v2 en la sección menor s2.
 
Por otra parte , el elemento de fluído delimitado por las secciones S1 y S2 esta en contacto con el aire a la misma presión, luego p1=p2=p0.
 
Finalmente, la diferencia entre alturas y1- y2 = H. siendo H la altura de la columna del fluído.
 
La ecuación de BErnoulli:
 
Con los datos del problema se escribirá de una formamás simple:
 
Publicado por en No hay comentarios:

TEOREMA DE BERNOULLI


Resultado de imagen para teorema de bernoulli
Cuándo la velocidad de un fluido en cualquier punto dado permanece constante en el transcurso del tiempo, se dice que el movimiento del fluido es uniforme. Esto es, en un punto dado cualquiera, en un flujo de régimen estable la velocidad de cada partícula de fluido que pasa es siempre la misma. En cualquier otro punto puede pasar una partícula con una velocidad diferente, pero toda partícula que pase por este segundo punto se comporta allí de la misma manera que se comportaba la primera partícula cuando pasó por este punto. Estas condiciones se pueden conseguir cuando la velocidad del flujo es reducida. Por otro lado, en un flujo de régimen variable, las velocidades son función del tiempo. En el caso de un flujo turbulento, las velocidades varían desordenadamente tanto de un punto a otro como de un momento a otro.
Resultado de imagen para teorema de bernoulli
ECUACIÓN DE BERNOULLI
La dinámica de los líquidos, está regida por el mismo principio de la conservación de la energía, el cual fue aplicado a ellos por el físico suizo Daniel Bernoulli (1700-1782), obteniendo como resultado una ecuación muy útil en este estudio, que se conoce con su nombre.
Para ello se puede considerar los puntos 1 y 2, de un fluido en movimiento, determinando la energía mecánica de una porción de éste, a lo largo del filete de fluido en movimiento que los une.
Si m es la porción de masa considerada, Aplicaciones del Teorema de Bernoulli
su rapidez, Aplicaciones del Teorema de Bernoulli
la altura sobre el nivel tomado como base, Aplicaciones del Teorema de Bernoulli
la presión y Aplicaciones del Teorema de Bernoulli
la densidad en cada uno de los puntos, se puede escribir utilizando el teorema trabajo-energía cinética:
Aplicaciones del Teorema de Bernoulli
Si ahora se divide a todos los términos de los dos miembros, entre la masa considerada, se obtendrá la ecuación de Bernoulli, que corresponde a la ley de la conservación de la energía por unidad de masa. Si el fluido es incompresible, como supondremos en lo sucesivo, dondeAplicaciones del Teorema de Bernoulli
, la ecuación de Bernoulli adopta la forma:
Aplicaciones del Teorema de Bernoulli
(6.10)
Así como la estática de una partícula es un caso particular de la dinámica de la partícula, igualmente la estática de los fluidos es un caso especial de la dinámica de fluidos. Por lo tanto, la ecuación (6.10) debe contener a la ecuación (6.5) para la ley de la variación de presión con la altura para un fluido en reposo. En efecto, considerando un fluido en reposo, y reemplazando Aplicaciones del Teorema de Bernoulli
en la ecuación de Bernoulli, se obtiene:
Aplicaciones del Teorema de Bernoulli
que es precisamente la ecuación fundamental de la estática de fluidos.
Ejemplos:
  • La presión del agua que entra a un edificio es 3 atmósfera, siendo el diámetro de la tubería 2[cm] y su rapidez de Aplicaciones del Teorema de Bernoulli
    . Si el baño de un departamento del 4º piso está a 6[m] de la entrada y la tubería tiene un diámetro de 4 [cm], calcule:
  • La presión y rapidez del agua en el baño,
  • La presión en el baño si se corta el agua a la entrada.
    • Solución.
    a. Usando la ecuación de Bernoulli a la entrada (región 1) y en el baño del 4º piso (región):
    Aplicaciones del Teorema de Bernoulli
    ,
    y la ecuación de continuidad,
    Aplicaciones del Teorema de Bernoulli
    ,
    donde Aplicaciones del Teorema de Bernoulli
    , Aplicaciones del Teorema de Bernoulli
    , Aplicaciones del Teorema de Bernoulli
    y Aplicaciones del Teorema de Bernoulli
    encontramos:
    Aplicaciones del Teorema de Bernoulli
    Aplicaciones del Teorema de Bernoulli
    Aplicaciones del Teorema de Bernoulli
    b. Si el agua se corta en la entrada, donde Aplicaciones del Teorema de Bernoulli
    ,
    Aplicaciones del Teorema de Bernoulli
    APLICACIONES DEL TEOREMA DE BERNOULLI JUNTO CON EL TUBO DE VENTURI.-
    La utilización de un tubo de Venturí en el carburador de un automóvil , es un ejemplo familiar del teorema de Bernoulli. La presión del aire, que pasa a través del cuerpo del carburador, disminuye cuando pasa por un estrangulamiento. La disminución de presión permite que fluya la gasolina, se vaporice y se mezcle con la corriente de aire.
    • TUBO DE VENTURI
    Un venturi es un dispositivo que clasicamente incorpora una simple convergencia y divergencia a travez de una sección y usa los principios de Bernoulli para relacionar la velocidad con la presión del fluido. Este principio se basa en que cuando el gas o liquido en movimiento, baja su presión y aumenta su velocidad.
    Un tubo de venturi es usado para medir la velocidad del flujo de un fluido. En la garganta, el area es reducida de A1 a A2 y su velocidad se incrementa de V1 a V2. En el punto 2, donde la velocidad es máxima, la presión es mínima. Esto lo sabemos de la ecuación de Bernoulli.
    Este dispositivo se utiliza para medir el gasto de una tubería. Al escurrir el fluido de la tubería a la garganta, la velocidad aumenta notablemente, y en concecuencia, la presión dismiuye; el gasto transportado por la tubería en el caso de un flujo incompresible esta en función de la lectura del manómetro.
    Las presiones en la seccion 1 y en la garganta (sección 2) son presiones reales, en tanto que las velocidades correspondientes obtenidas en la ecuación de Bernoulli sin un término de pérdidas son velocidades teóricas. Si se consideran las pérdidas en la ecuación de la energía entonces se trata de velocidades reales. En lo que sigue se obtendrá primero la velocidad teórica en la garganta al aplicar la ecuación de Bernoulli sin el término de pérdidas. Multiplicando este valor por el coeficiente Cv, se determinará la velocidad real. Esta última, multiplicada por el área real de la garganta, permite obtener el gasto que circula por la tubería.
    Nota: Para obtener resultados precisos, el tubo de Venturi debe estar precedido por una longitud de al menos diez veces en diametro de la tubería.
    Donde V1, V2, p1 y p2 son las velocidades y presiones en las secciones 1 y 2 respectivamente. Esta ecuación incorpora la concervación de la energía para fluidos.
    Usaremos la ecuación de continuidad para flujo de fluidos. Esta se basa en que con ausencia de pérdida de masa, el flujo de fluido que entra en una región dada debe ser igual al que sale.
    Para flujo incompresible:
    Juntando la ecuación de Bernoulli con la de continuidad, se tendrá:
    Por otro lado la diferencia manométrica h se puede relacionar con la diferencia de presiones al escribir la ecuación del manómetro. De este modo se obtiene una expresión para el gasto.
    Donde S0 es la gravedad específica del liquido en el manómetro y S1 es la gravedad específica del líquido a travez de la tubería. Esta expresión que constituye la ecuación del tubo de venturi para flujo incompresible. El gasto depende de la diferencia manométrica h.
    El coeficiente Cv se determina mediante un método de calibración (número de Reynolds).
    • Aplicando la ecuación de Bernoulli y continuidad en los puntos 1 y 2, los cuales están a una misma altura:
    Aplicaciones del Teorema de Bernoulli
    (1)
    Aplicaciones del Teorema de Bernoulli
    (2)
    Reemplazando (2) en (1), encontramos:
    Aplicaciones del Teorema de Bernoulli
    .
    Despejando, por ejemplo, Aplicaciones del Teorema de Bernoulli
    , se tiene:
    Aplicaciones del Teorema de Bernoulli
    (3)
    Por otro lado, usando el manómetro para determinar la diferencia de presiones Aplicaciones del Teorema de Bernoulli
    , encontramos que como los niveles A y B están a una misma altura:
    Aplicaciones del Teorema de Bernoulli
    , es decir:
    Aplicaciones del Teorema de Bernoulli
    Por lo tanto,Aplicaciones del Teorema de Bernoulli
    , que al reemplazar en ecuación (3) resulta:
    Aplicaciones del Teorema de Bernoulli
    Publicado por en  
    Publicado por en No hay comentarios:

    Ecuación de continuidad

    ECUACIÓN DE CONTINUIDAD

    En física, una ecuación de continuidad expresa una ley de conservación de forma matemática, ya sea de forma integral como de forma diferencial.

    Teoría electromagnética

    En teoría electromagnética, la ecuación de continuidad viene derivada de dos de las ecuaciones de Maxwell. Establece que la divergencia de la densidad de corriente es igual al negativo de la derivada de la densidad de carga respecto del tiempo:
    En otras palabras, sólo podrá haber un flujo de corriente si la cantidad de carga varía con el paso del tiempo, ya que esta disminuye o aumenta en proporción a la carga que es usada para alimentar dicha corriente.
    \nabla \cdot \vec{J} = - {\partial \rho \over \partial t}
    Esta ecuación establece la conservación de la carga.

    Mecánica de fluidos

    En mecánica de fluidos, una ecuación de continuidad es una ecuación de conservación de la masa. Su forma diferencial es:
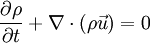
    {\partial \rho \over \partial t} + \nabla \cdot (\rho \vec{u}) = 0
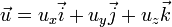    donde  \rho  es la densidad, t el tiempo y \vec{u} = u_x \vec i + u_y \vec j + u_z \vec k la velocidad del fluido. Es una de las tres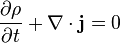 ecuaciones de Euler.

    Mecánica cuántica[editar]

    En Mecánica cuántica, una ecuación de continuidad es una ecuación de conservación de la probabilidad. Su forma diferencial es:1
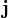    \frac {\partial \rho}{\partial t} + \nabla \cdot \mathbf{j} = 0
    Donde  \rho  es la densidad de probabilidad de la función de ondas y  \mathbf{j}  es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con lafunción de onda de una partícula como:
    \rho=|\Psi|^2=\Psi^*(\mathbf{r},t)\Psi(\mathbf{r},t), \quad \mathbf{j} = {i \over 2m} \left( \Psi^*\boldsymbol{\nabla}\Psi - \Psi\boldsymbol{\nabla}\Psi^* \right)\,\!

    Mecánica relativista[editar]

    En la teoría especial de la relatividad, una ecuación de continuidad debe escribirse en forma covariante, por lo que la ecuación de continuidad usual para la carga eléctrica y otras magnitudes conservadas se suele escribir en teoría de la relatividad como:
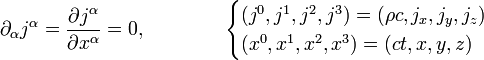
    \part_\alpha j^\alpha = \frac{\part j^\alpha}{\part x^\alpha} = 0, \qquad \qquad \begin{cases} (j^0, j^1, j^2, j^3) = (\rho c, j_x, j_y, j_z)\\ (x^0,x^1,x^2,x^3) = (ct, x, y, z) \end{cases}
    La ecuación de continuidad para la densidad másica (o más exactamente la energía másica) y la densidad de momento lineal se escribe en términos del tensor energía impulso:
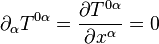
    \part_\alpha T^{0\alpha} = \frac{\part T^{0\alpha}}{\part x^\alpha} = 0
    En el contexto de la teoría general de la relatividad las derivadas parciales deben substituirse por derivadas covariantes:
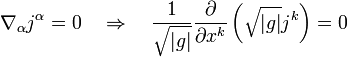
    \nabla_\alpha j^\alpha = 0 \quad \Rightarrow \quad \frac{1}{\sqrt{|g|}} \frac{\part}{\part x^k} \left(\sqrt{|g|} j^k \right) = 0
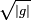    Donde \scriptstyle \sqrt{|g|} es la raíz del determinante del tensor métrico asociado a las coordenadas \scriptstyle x^\alpha. Y análogamente para la conservación de la energía:
    \nabla_\alpha T^{0\alpha} = 0
    Publicado por en No hay comentarios:
    Suscribirse a: Entradas (Atom)